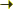 Help
Help
Bilbao Crystallographic Server
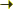 Help Help
|
|
The electric field can be represented as a vector. A vector is invariant under the rotations along
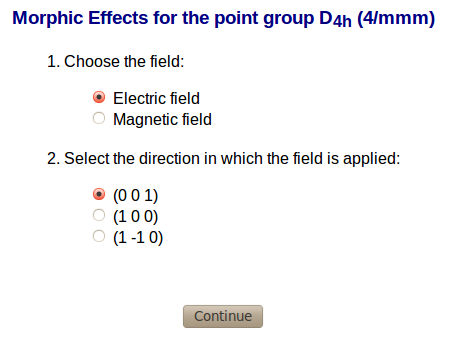
its axes, the planes which contains that vector leave also it invariant as one can observe in the figure. Taking this into account one can say that there are infinity rotations and planes which leave the vector invariant. In this case, a vector can be represented by the point group: C∞v (∞m). One can calculate the new point group of the crystal + electric field by the intersection of the initial point group (G) and the point group which represent the electric field (GE): where GE is the point group C∞v (∞m) and G' is the point group of the crystal + electric field and it is a subgroup of the initial point group. Example: Supose that the point group of the crystal without electric field is G = D4h (4/mmm) and it is applied an electric field along the direction (0 0 1). The point group of the crystal with an electric field applied is: Imagine that the electric field is applied in the direction (1 0 0): Once the point group of the extended system is known it is easy to calculate the correlation relations between the point groups and their behaviour. |
|
|
The magnetic field can be represented as an axial vector or a pseudovector. An axial vector is invariant
under the rotations along its axes, the plane perpendicular to this axes also leaves invariant the axial vector as it is shown in the figure. Taking this into account one can say that there are infinity rotations and one perpendicular plane which leave an axial vector invariant. In this case, a vector can be represented by the point group: C∞h (∞/m). One can calculate the new point group of the crystal + magnetic field by the intersection of the initial point group (G) and the point group which represent the magnetic field (GM): where GM is the point group C∞h (∞/m) and G' is the point group of the crystal + magnetic field and it is a subgroup of the initial point group. Example: Supose that the point group of the crystal without magnetic field is G = D4h (4/mmm) and it is applied a magnetic field along the direction (0 0 1). The point group of the crystal with a magnetic field applied is: Imagine that the magnetic field is applied in the direction (1 0 0): One the point group of the extended system is known it is easy to calculate the correlation relations between the point groups and their behaviour. |
|
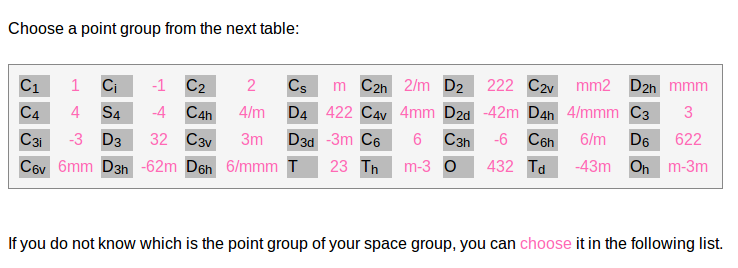
One can select directly the point group from the table, one can also select the space group.
The next page is where one have to select the field (electric or magnetic) and the direction in which is going to be applied.
In this part of the output one can find which are the parameters one has introduced: the filed, the direction and the point group.

There is a direct link to the program POINT which gives us information about the initial point group (character tables, point subgroups, ...).
Here one can find which is the new point group of the crystal + applied field and the transformation matrix which relates the initial whit the final point group.

There is another direct link to the program POINT which gives us information about the reduced point group (character tables, point subgroups, ...).
In the last part of the output one can find the correlation relations between the initial crystal and the extended one.
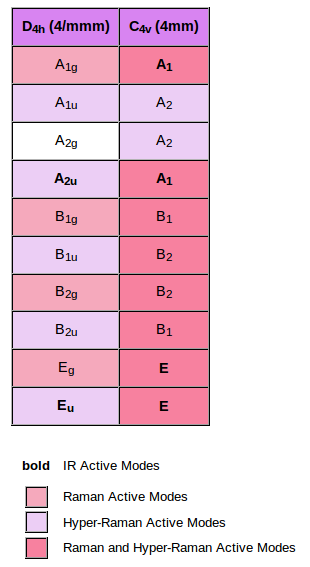
|
Taking into account this table, one can say:
Using this table one can predict the behaviour of the modes when it is applied and external field in a certain direction. |
|
Bilbao Crystallographic Server www.cryst.ehu.es |
For comments, please mail to administrador.bcs@ehu.es |