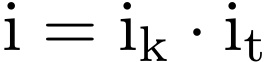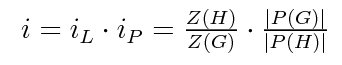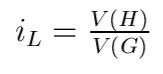Foreach pair of space groups G > H, a uniquely defined space group M exist such that H ≤ M ≤ G where:
- M is a t-subgroup (translationengleich subgroup) in G: [ it ] is the t-index of M in G
- H is a k-subgroup (klassengleich subgroup) in M: [ ik ] is the k-index of H in M
M is called the Hermann group.
The Hermann Theorem can distinguish between three types of subgroups:
- t-subgroups (or translation equivalent subgroups):
If H is a t-subgroup of G means that T(H) = T(G), i.e. the translation groups of G and H are the same.
The subgroup H loses rotation type operations with repect to G and therefore the point group P(H) < P(G)
M is equal to H.
- k-subgroups (or point group equivalent subgroups):
If H is a k-subgroup of G means that P(H) = P(G), i.e. the point groups P(G) and P(H) are the same.
The subgroup H loses translation type operations with repect to G and therefore the translation group T(H) < T(G)
M is equal to G.
- general type subgroups: T(H) < T(G) and P(H) < P(G) and so, H < M < G
As consequence a maximal subgroup is always or t-subgroup or k-subgroup of the initial group.
The index of a transformation in a group-subgroup (G > H) relation can be factorized in two parts according to the Hermann theorem.
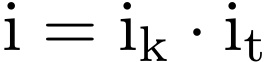
In the formula, [ ik ] is the k-index (the klassengleich index), which coincides with the cell multiplication in the subgroup in the case of primitive cells, and [ it ] (the translationengleich index), which is equal to the ratio between the orders of the point groups of G and H.
In terms of the corresponding indices:
- t-subgroups (or translation equivalent subgroups): ik = 1, then it = i
- k-subgroups (or point group equivalent subgroups): it = 1, then ik = i
- general type subgroups: ik ≠ 1 and it ≠ 1
An alternative notation in use for [ ik ] is [ iL ] and for [ it ] is [ iP ].
The index of a transformation is related with the number of formula units of the two structures whose symmetry groups are group-subgroup related.
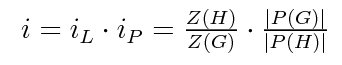
In the given formula [ i ] is the index of the transformation, |P(G)| and |P(H)| are the orders of the point groups of the corresponding space groups G and H and Z(G), Z(H) are the number of formula units per primitive unit cell of two structures with symmetry groups G and H. The index [ iL ] is also equal to the ratio of volume of the primitive unit cell of H and G:
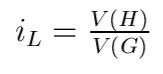
Example 1:
Consider the phase transition between tetragonal P4mm (99) and cubic Pm-3m (221) structures of BaTiO3. The number of formula units per primitive unit cell are equal to Z(G) = Z(H) = 1. The two phases are group-subgroup related, and a valid index for this transformation according to the formula is equal to the ratio between the orders of the point groups |P(G)| / |P(H)|. The order of a point group is just the number of the elements of the point group. The ratio between the orders of the point groups can be obtained from the program POINT. The valid index for this transformation is 6.
[ Check the P4mm subgroups of space group Pm-3m with index 6 ]
Example 2:
Consider the group-subgroup related phase transition between orthorhombic Pnma (62) and Pna21 (33) phases of K2SeO4. The number of formula units per primitive unit cell for the given structures are Z(G) = 4 and Z(H) = 12. The orders of the point groups are |P(G)| = 8 and |P(H)| = 4. A simple application of the formula gives an index 6 for this transformation.
[ Check the Pna21 subgroups of space group Pnma with index 6 ]
Example 3:
Consider the group-subgroup related phase transition between monoclinic C2/c (15) and P21/c (14) phases of CaTiSiO5. The number of formula units per primitive unit cell for the given structures are Z(G) = 2 and Z(H) = 4. A simple application of the formula gives an index 2 for this transformation.
[ Check the P21/c subgroups of space group C2/c with index 2 ]
- Orientational (twin) domains: As a consequence of a lost of rotational elements
- Antiphase domains: As a consequence of a lost of translational elements
[ it ] is the number of twin domains and [ ik ] is the number of antiphase domains.
Example 1:
Quartz P6222 (180) > P3221 (154) with index 2
ik = 1 , i = it = 2. P3221 is a t-subgroup of P6222. Twin domains.
[ Check the t-subgroups of space group P6222]
Example 2:
Cu3Au: Fm-3m (225) > Pm-3m (221) with index 4
it = 1 , i = ik = 4. Pm-3m is a k-subgroup of Fm-3m. Antiphase domains.
[ Check the k-subgroups of space group Fm-3m ]
Example 3:
β - Gd2(MoO4)3: P-421m > Pba2 with index 4
it = 2 , ik = 2. Pba2 is a general type subgroup of P-421m. Twin and antiphase domains.
 Help
Help
 Help
Help